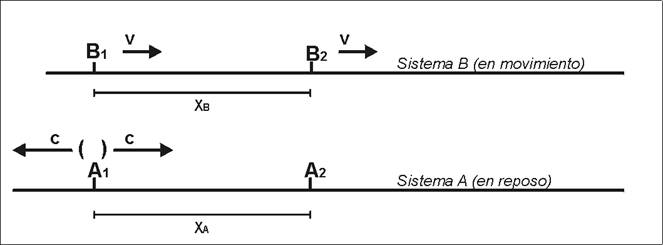
Fig. 1 - En el sistema en reposo la señal luminosa "( )" viaja a velocidad "c" en todas direcciones
(Primer desarrollo: 04 de
abril de
2003
Última modificación: 02 de agosto de 2005)
En el Capítulo IV del libro "La Relatividad Conceptual" se analizaron, tanto la formulación matemática como las consecuencias de las transformadas de Lorentz, sobre las mediciones de longitudes y tiempos, para sistemas con movimiento relativo.
Como se vio, estas transformadas adoptan la siguiente expresión matemática:
t’ = (t - vx/c2)/K
x’ = (x -vt)/K
y’=y
z’=z.
Donde K = (1 - v2/c2)0.5.
Con ellas se describe la relación entre las lecturas de longitudes y tiempos que realizan los observadores de un determinado sistema inercial (x, y, z, t) y los valores (x’, y’, z’, t’) que se miden en otro sistema inercial que se mueve, con respecto a ellos, a velocidad v
La inversión de los cálculos conduce a la expresión de las coordenadas del eje estacionario respecto de los valores registrados en el eje móvil
t = (t' + vx'/c2)/K
x = (x' + vt')/K
y = y'
z = z'
Nota: En las fórmulas inversas, el cambio de signo obedece a que la velocidad relativa conserva el valor absoluto, pero con el sentido contrario.
Empleando los dos postulados de la Relatividad Especial, en el trabajo de 1905 Einstein hizo los desarrollos adecuados para llegar a estas ecuaciones. Sin embargo, en este apéndice quiero recorrer un camino algo diferente para destacar que las transformadas de Lorentz también describen un modelo con un Marco de Referencia Localmente Estacionario (MRLE), en el que la velocidad de las ondas electromagnéticas, aunque diferente para cada sistema inercial, aparenta tomar el valor c para todos ellos.
No obstante, como se verá, los postulados que se emplean en este apéndice son los mismos que empleó Einstein en 1905. Estos postulados se presentan como resultados impuestos por las mediciones experimentales.
Durante el desarrollo se comprueba que no es necesario eliminar los marcos de referencia privilegiados para demostrar que el movimiento "absoluto" es indetectable mediante experiencias ordinarias. Este enfoque muestra, adicionalmente, que distintos modelos pueden conducir a las mismas ecuaciones.
De modo que vamos a estudiar el ejemplo esquematizado en la Fig. 1, donde:
Suponemos que existe un MRLE en el que la velocidad de la luz es la misma en todas las direcciones (c = 300,000 km/s). A efectos de clarificar los conceptos, el MRLE se comporta en forma equivalente a una masa de aire estacionaria que hace de soporte para la transmisión de ondas sonoras.
Elegimos un sistema (llamado A), que permanece en reposo con respecto al MRLE.
Sobre el sistema A existen numerosos observadores con relojes sincronizados mediante señales luminosas. La sincronización está hecha de tal modo que una foto "instantánea", tomada con una cámara "mágica" (que recibe señales no limitadas por la velocidad de la luz) mostraría una situación como la ejemplificada en la Fig. 2.
Solidarios al sistema A, elegimos dos observadores A1 y A2, separados por una distancia XA. En realidad A1 y A2 "saben" que están a dicha distancia en base el tiempo que tarda la luz (a velocidad c) en recorrer la distancia que los separa.
Elegimos un segundo sistema (al que llamamos B) que se desplaza a una velocidad v con respecto al sistema A.
En el sistema B identificamos dos observadores (B1 y B2) que se enfrentan con A1 y A2 cuando los relojes del sistema A marcan el tiempo inicial del experimento (T = 0).
Adicionalmente suponemos que el reloj de B1 también marca T = 0 al enfrentarse con A1 (Fig. 2).
|
|
|
Fig. 1 - En el sistema en reposo la señal luminosa "( )" viaja a velocidad "c" en todas direcciones |
En la Fig. 1 se muestran dos rayos luminosos, identificados con "(" y ")", que parten desde la posición del observador A1. Ambos rayos se desplazan realmente a la velocidad c de 300,000 km/s en el MRLE. Con respecto al sistema B, estos rayos se desplazan a la velocidad "c-v" en el sentido del desplazamiento de B, y "c+v" en sentido contrario.
Nota: El modelo que adoptamos tiene un Marco de Referencia Estacionario por lo que resulta válido decir que un rayo de luz se desplaza realmente a determinada velocidad. La percepción que los distintos observadores tengan de esta velocidad verdadera es lo que llamaremos velocidad aparente. En el sistema A la velocidad real y la velocidad aparente son coincidentes. Lo mismo ocurre con los tiempos y distancias. Aceptamos, por lo tanto, que las mediciones hechas en el sistema A se corresponden con los valores reales de estas magnitudes. En otras palabras, las observaciones de A coinciden con las imaginarias fotografías mágicas del experimento.
Como ya se discutió a lo largo de la obra citada, la convención con respecto a valores reales y aparentes está en total desacuerdo con los conceptos relativistas, donde cada observador de un sistema inercial puede reclamar, con total derecho, que sus mediciones son las verdaderas. De todos modos, la existencia de un marco de referencia inmóvil está más en concordancia con la experiencia de ondas que se trasladan en un medio soporte. Al final del desarrollo se discuten las diferencias entre uno y otro punto de vista.
|
|
|
Fig. 2: Marcha de los relojes en el instante en que se enfrentan los observadores. Como veremos, la lectura del reloj del observador B2 no puede establecerse "a priori". |
La Fig. 2 muestra las lecturas de los distintos relojes en el momento en que A1 enfrenta a B1 y que A2 enfrenta a B2. Tal como se indicó, por razones de simplicidad, se supone que los relojes de A1 y de B1 tienen lecturas coincidentes, pero no puede suponerse lo mismo para las lecturas de A2 y B2.
Para los observadores del sistema A, de acuerdo con la Fig. 1, la distancia entre B1 y B2 es idéntica a la distancia que separa a A1 de A2. A esta distancia la llamamos XA, y conforme al modelo que estamos empleando, ese valor es el valor verdadero de dicha magnitud.
La luz tarda XA / c segundos en hacer el recorrido entre A1 y A2 y emplea también XA / c segundos en cubrir el trayecto de Vuelta (de A2 hacia A1). El tiempo total que emplea la luz para realizar el trayecto de ida y vuelta entre A1 y A2 (que llamaremos T0A) es, por lo tanto:
T0A = 2 XA / c [1]
Por otro lado, cuando la luz parte hacia B2 (el rayo de la derecha en la Fig. 1) recorre la distancia B1-B2 a la velocidad "c-v", ya que el sistema móvil se está alejando de la posición (absoluta) de la que fue emitida la señal.
Por lo tanto para los observadores de A, podemos escribir:
T1A = XA / (c-v) [2]
En la ecuación [2], T1A representa el tiempo que tarda la señal luminosa en hacer el recorrido B1-B2, de acuerdo con los relojes de los observadores del eje A.
Y cuando la señal retorna a B1 emplea:
T2A = XA / (c+v) [3]
Siempre de acuerdo con las mediciones de los observadores del sistema A.
De modo que el tiempo que toma la señal en partir de B1, alcanzar la posición de B2 y retornar a B1, según lo miden desde el sistema A, resulta:
T3A = T1A + T2A = XA / (c-v) + XA / (c+v) [4]
Y, reagrupando los términos de [4], obtenemos
T3A = (2 XA / c ) / (1 - v2/c2 ) [5]
En la que 2 XA / c puede reemplazarse por su equivalente en [1], de modo de obtener
T3A = T0A / (1 - v2/c2 ) [6]
La Ecuación [6] muestra la relación entre el tiempo (T0A) que tarda el rayo luminoso en recorrer (en un camino de ida y vuelta) una longitud estacionaria y el tiempo (T3A) que emplea para la misma longitud, cuando ésta se desplaza a velocidad v. Los cálculos son realizados desde el sistema A y corresponden a un análisis absolutamente clásico (“Newtoniano”) del sistema.
En la Fig. 1 identificamos como XB al valor que obtienen los observadores del sistema B cuando miden la distancia que separa a B1 de B2. El valor XB puede ser diferente del valor verdadero (XA) de modo que podemos escribir:
XA / XB = K [7]
Donde K es un valor a determinar.
Nota: La ecuación [7] plantea una posible relación lineal entre XA y XB, pues cualquier otra relación permitiría detectar las deformaciones, desde el propio sistema móvil, con una regla de longitud fija. Ejemplo: Si una longitud de 1 metro se alterara en una fracción diferente a una de 100 metros, con una regla de 1 metro no se detectarían cambios en la primera longitud, pero sí en la segunda. Y ese cambio permitiría detectar, mediante un experimento interno (hecho en el propio sistema inercial) que el sistema inercial no está en reposo.
El valor K expresa la posible diferencia de apreciación de una misma distancia, realizada por observadores en diferentes sistemas de referencia. Tal como se construyó el modelo, resulta que la medición realizada en el eje A es la medición "verdadera". De esta forma si K resulta ser diferente de la unidad, debemos concluir que las mediciones realizadas en el eje B se alteran como resultado de su movimiento respecto al MRLE.
Basándose en las experiencias de Michelson y Morley y otras que emplean mediciones con recorridos de ida y vuelta del rayo luminoso, podemos establecer como hecho experimental muy sólido que:
Enunciado 1: En todos los sistemas inerciales (no sometidos a aceleraciones) se obtiene el mismo valor para la velocidad de las ondas electromagnéticas en recorridos de ida y vuelta de la señal.
Pregunta: ¿Éste no es el segundo postulado de Einstein sobre la constancia de la velocidad de la luz?
Respuesta: Tal como está redactado este enunciado difiere del postulado de la constancia de la velocidad de la luz en que lo que se acepta como constante no es la velocidad de la luz sino el valor numérico del cociente entre espacio recorrido y tiempo empleado por la luz durante la medición experimental.
Pregunta: Pero... ¿Existe alguna diferencia entre ambos enunciados?
Respuesta: Si. No es lo mismo decir que la velocidad de la luz es constante, a afirmar que lo único que es constante es el resultado del cálculo. De este modo los 300,000 km/s pueden ser el resultado de una longitud y un tiempo alterados proporcionalmente por el movimiento.
Pregunta: Pero... ¿Es posible que las distancias y las tiempos se deformen adecuadamente para mantener un resultado constante aunque la velocidad de la luz no lo sea?
Respuesta: Si. No sólo es posible, como veremos en este desarrollo, sino que es justamente lo que debería esperarse si la velocidad de las ondas electromagnéticas estuviera ligada íntimamente a la estructura interna de la materia. Algo así planteó Lorentz para justificar el resultado negativo del experimento de Michelson, como puede apreciarse en la cita introductoria de este apéndice.
………………
El enunciado 1 pone ciertas restricciones para que el modelo que estamos desarrollando sea válido. Los observadores del eje móvil deben obtener el valor c = 300,000 km/s cuando realizan sus experiencias para medir la velocidad de la luz en recorridos de ida y vuelta. Esto equivale a afirmar que si llamamos T0B al tiempo que tarda la luz en recorrer la distancia de B1 hasta B2 y retornar a B1 (recorriendo dos veces la longitud XB) debe cumplirse que:
2 XB / T0B = c [8]
En [8] todos los valores están medidos por observadores solidarios al sistema B. Como ya se expresó, este resultado no significa que la velocidad de la luz sea constante, sino que se obtiene un valor constante para el cociente entre un tiempo que puede estar alterado y una longitud que también puede estarlo.
Igualando los primeros términos de las expresiones [1] y [8] obtenemos
2 XB / T0B = 2 XA / T0A
Donde simplificando y reordenando los términos resulta
T0B / T0A = XB / XA [9]
De modo que, de acuerdo con [6]
T0B / T3A = (1 - v2/c2 ) XB / XA [10]
Donde, reemplazando XB / XA por su equivalente expresado en [7]
T0B / T3A = (1 - v2/c2 ) / K [11]
Siendo T3A y T0B los tiempos empleados en ambos sistemas para caracterizar la duración de un mismo evento (la ida y vuelta de una señal luminosa desde la posición de B1 hasta la posición de B2). De este modo las ecuaciones [7] y [11] establecen las relaciones existentes entre los valores de longitudes y tiempos medidos en ambos sistemas.
Para obtener el valor de K sólo es necesario notar que, si existen alteraciones en los parámetros medidos, para mantener constante el cociente entre longitudes y tiempos, ambos deben variar en la misma proporción.
De acuerdo con [7] sabemos que la distancia real B1-B2 es K veces la distancia que detectan los observadores del sistema B. Por lo tanto, el tiempo que transcurre durante la experiencia de ida y vuelta del rayo luminoso también debe ser K veces el tiempo "real" (medido en el sistema A, solidario al MRLE). Por esta razón,
T0B / T3A = K [12]
Y reemplazando [12] en [11] obtenemos:
K2 = (1 - v2/c2 ) [13]
O su equivalente,
K = (1 - v2/c2 ) 0.5 [14]
La ecuación [14] no es más que la expresión del coeficiente de Lorentz.
Conforme a la ecuación [7], para satisfacer la constancia de c en sistemas en movimiento, las mediciones de longitudes realizadas en ese sistema deben estar alteradas. Como K es menor que la unidad, las longitudes medidas en B resultan mayores que las que se miden desde A. En otras palabras, desde A se detectan, en el sistema B, longitudes menores que las que declaran los propios observadores del sistema B. En consecuencia, las varillas del sistema móvil resultan más cortas cuando se miden desde el sistema estacionario. El factor que relaciona ambas longitudes es el coeficiente de Lorentz (K).
Conforme a la ecuación [12], para satisfacer la constancia de c en sistemas en movimiento, las mediciones de intervalos temporales realizadas en ese sistema también deben estar alteradas. Como K es menor que la unidad, los intervalos medidos en B resultan menores que los que se miden en A, para un mismo evento. En otras palabras, desde A se miden, intervalos temporales mayores que los que detectan los observadores del sistema B. Por lo tanto, los relojes de B deben marchar más lentamente que los de A. El factor que relaciona la marcha de ambos relojes es, nuevamente, el coeficiente de Lorentz.
Dado que la medición de la velocidad de la luz arroja un valor constante en mediciones de ida y vuelta y nunca se han obtenido indicaciones directas o indirectas respecto a la dependencia de c con el sentido de desplazamiento, podemos suponer que:
Enunciado 2: Los sistemas físicos se integran al universo de modo que el valor de la velocidad de la luz también arroje un valor constante para mediciones hechas en recorridos en un solo sentido (caminos de Ida o Vuelta únicamente).
Pregunta: ¿Qué hizo Einstein con estos valores durante el desarrollo de la Relatividad especial?
Respuesta: Postuló (tal como hemos hecho en este desarrollo) que ambos valores eran idénticos como base de su metodología para sincronizar relojes distantes.
Pregunta: Pero... en el modelo presentado en estos desarrollos “sabemos” que ambos valores son diferentes. De acuerdo con el modelo, la velocidad de la luz con respecto al eje B es (c+v) o (c-v) según el sentido de desplazamiento del rayo luminoso. ¿Cómo puede parecer que ambos tiempos son iguales?
Respuesta: Alterando las lecturas de los relojes para que los observadores del sistema B, crean que los tiempos son iguales.
Pregunta: Pero... esto es hacer trampa. ¿Con qué objeto los relojes de B se alterarían para engañar a sus propios observadores?
Respuesta: El planteamiento es inverso. Como se discutió en el capítulo IX, en forma natural se deforman las lecturas de los relojes (y cosas mucho más profundas, ligadas a la estructura íntima de la realidad) de modo que los observadores en movimiento no se dan cuenta que se están moviendo. Es algo parecido a la equivalencia de sistemas inerciales planteada por Galileo. Parece una propiedad de nuestro Universo que los observadores no pueden detectar fácilmente su movimiento absoluto.
.........................
Con este nuevo enunciado podemos resolver el sistema planteado.
Empecemos por determinar cuál es la lectura del reloj de B2 si los relojes de B1 y de A1 tienen la misma lectura (tal como se muestra en la Fig. 2)
Para eso llamaremos:
T1B: Tiempo empleado por la luz para recorrer el trayecto B1-B2, medido en el sistema B.
T2B: Tiempo empleado por la luz para recorrer el trayecto B2-B1, medido en el sistema B.
De modo que
T0B = T1B + T2B [15]
Donde, reemplazando T0B despejado de la ecuación [8], resulta
T1B + T2B = 2 . XB / c [16]
Y como la distancia a recorrer es la misma en ambos sentidos, los tiempos empleados son inversamente proporcionales a la velocidad de la luz en cada tramo, de modo que:
T1B / T2B = (c+v) / (c+v) [17]
Donde, despejando T1B entre [16] y [17] obtenemos
T1B = XB (c+v) / c2 [18]
De este modo, la expresión [18] establece el tiempo que tarda el rayo luminoso para recorrer la distancia B1-B2 en función de la velocidad del eje B y del valor asignado en dicho sistema a la distancia que separa ambos observadores.
Sin embargo, conforme a nuestro segundo postulado debe cumplirse que:
T1B = T0B / 2 [19]
Donde, reemplazando T0B por su equivalente según [8], resulta:
T1B = XB / c [20]
La diferencia entre el valor de T1B calculado en las expresiones [18] y [20] tiene el siguiente significado:
La expresión [18] muestra el intervalo de tiempo que transcurre realmente en el sistema B mientras el rayo de luz recorre el trayecto B1-B2.
La expresión [20] indica la diferencia de lecturas que debe obtenerse entre el reloj de B1 cuando parte la señal y el reloj de B2 cuando la señal alcanza su posición para que ambos observadores coincidan en apreciar que el tiempo empleado en el trayecto de ida es la mitad del tiempo total empleado en el recorrido de ida y vuelta.
Por lo tanto, si denominamos
TB1i a la lectura del reloj del origen de coordenadas en el momento que parte la señal.
TB2i a la lectura del reloj de B2 ubicado a una distancia XB del origen de coordenadas, en el momento que parte la señal.
TB2f a la lectura del reloj de B2 en el momento en que la señal llega a B2.
debe cumplirse, conforme a la ecuación [20]
TB2f = TB1i + XB / c [21]
Por lo tanto TB2i debe tomar el valor
TB2i = TB1i - XB (c+v) / c2 + XB / c [22]
para que XB (c+v) / c2 segundos después, su lectura sea la que indica la expresión [21]
En resumen. la expresión [22] indica la diferencia de lecturas que debe existir entre los relojes de los observadores B1 y B2 para que puedan mantener la apariencia de la constancia de c en el recorrido de la luz entre B1 y B2.
y, simplificando la expresión [22], obtenemos
TB2i = 0 - XB v / c2 [23]
Dado que hemos asumido que el reloj de B1 marca el tiempo TB1i =00 en el momento que parte la señal luminosa.
Y en base a [7] puede re-escribirse la ecuación [23] como
TB2i = - (XA v / c2 ) / K [24]
Que expresa la lectura de cualquier reloj del eje B, a tiempo t=00 y a una distancia XA, del origen de coordenadas de A.
Este atraso en la lectura del reloj de B2 con respecto al reloj de B1 también genera un valor aparente de c para la velocidad de la luz en el trayecto de vuelta (desde B2 hasta B1).
La Fig. 3 muestra la lectura de todos los relojes en el momento en que tanto A1 y B1 como A2 y B2 se enfrentan.
|
|
|
Fig. 3 – Relación de tiempos y distancias en el instante en que se enfrentan los observadores. |
Como se puede apreciar, los valores presentados en la Fig. 3 son los mismos que se obtienen con las transformadas de Lorentz, presentadas al comienzo de este apéndice, para t = t’ = 0 (cuando coinciden en lectura y posición, los relojes de ambos orígenes de coordenadas).
Adicionalmente, si se sustituyen las variables para cualquier otro tiempo, las expresiones también coinciden con las transformadas de Lorentz.
Si bien en esta página se analizó el comportamiento de longitudes y tiempos en el eje móvil, tomando como "reales" las mediciones hechas en el eje estacionario, ya se mencionó que las ecuaciones de Lorentz son "reversibles". De este modo resulta que
Desde el eje estacionario se observa que las longitudes medidas en el eje móvil son menores que las que se miden en el eje estacionario y los relojes del eje móvil marchan más lentamente que los del eje estacionario.
Desde el eje móvil se observa que las longitudes medidas en el eje estacionario son menores que las que se miden en el eje móvil y los relojes del eje estacionario marchan más lentamente que los del eje móvil.
En el primer caso las observaciones son "reales" y en el segundo son "aparentes", pero los observadores de ambos sistemas de medición creen que son los observadores del otro sistema los que tienen resultados alterados.
Esta situación conduce a que no sea posible, por comparación de mediciones, detectar cuál de los dos sistemas es el solidario con respecto al MRLE y cuál es el eje realmente móvil. Este tema se analiza con un ejemplo muy detallado, en el Capítulo VI.
En este desarrollo se muestra que las ecuaciones de transformación entre longitudes y tiempos para sistemas en movimiento relativo uniforme pueden derivarse mediante un modelo "clásico" que considere la existencia de un Marco de Referencia Estacionario.
Al condicionar el modelo mediante dos enunciados que respetan los hechos experimentales, resulta que los observadores de los sistemas en movimiento no perciben las alteraciones que se producen en sus propios sistemas de medida. Este hecho está en concordancia con la expresión de Einstein "..... La introducción de un ´eter luminífero´ probará ser superflua ..." en su desarrollo de la Teoría de la Relatividad Especial, sólo que el significado de esta expresión no sería el que se le atribuye regularmente.
Mediante este modelo se muestra que no es necesario que desaparezca el Éter (o su equivalente en el marco de referencia), dado que su presencia no es detectable mediante experiencias ordinarias.
Y..., como se analiza en diferentes desarrollos a lo largo de este libro, hay una notable diferencia conceptual entre la no existencia de marcos de referencia y la imposibilidad de ponerlos de manifiesto.