La
"Equivalencia" de las Transformadas de Lorentz
para Sistemas Inerciales.
(Primer desarrollo: 04 de
abril de
2003
Última modificación: 02 de agosto de 2005)
En esta página se analiza un punto que no suele discutirse en los desarrollos de la Relatividad Especial. El tema no es trivial ni matemática ni conceptualmente, pero suele confundir a quienes trabajan con las transformadas de Lorentz.
Como ya se indicó en varias de las páginas de este sitio, las transformadas de Lorentz son las siguientes
Donde el juego de valores (t', x', y', z') está medido en el eje "móvil" (sistema B) y el juego (t, x, y, z) son los valores correspondientes del eje "estacionario" (sistema A).
Aunque no lo mencioné con anterioridad, quienes están familiarizados con este juego de ecuaciones, saben que las mismas son de aplicaciones para calcular los valores del eje B en función de los valores del eje A y también para calcular los valores del eje A en función de los valores propios del eje B. No podría ser de otra manera puesto que ambos sistemas inerciales gozan de las mismas propiedades conforme al primer postulado de la Relatividad Especial.
Nota: En el presente desarrollo se llega a las mismas conclusiones si los términos "movil" y "estacionario" se toman con significado relativo o con significado absoluto.
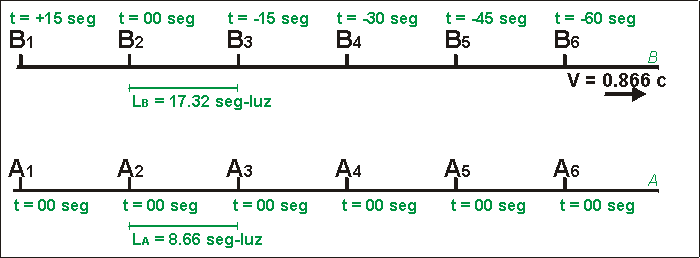
La Fig. 1 nos muestra una instantánea "mágica" del estado de cosas que describirían los observadores del sistema A cuando sus relojes marcan 00 seg y la velocidad relativa entre ambos ejes es de 0.866 c (con un coeficiente de Lorentz de 0.5).
 |
| Fig. 1 - Descripción del estado de los relojes en ambos sistemas (a t=00), de acuerdo con los observadores del eje A. |
La Fig. 1 no es más que un esquema típico de los que aparecen en los libros de relatividad cuando se ejemplifica lo que se suele llamar el "Lío de los relojes".
El problema que quiero analizar en esta página es que, en los mismos libros, suele emplearse algo parecido a la Fig.2 para describir las cosas tal como las ven los observadores del eje B.
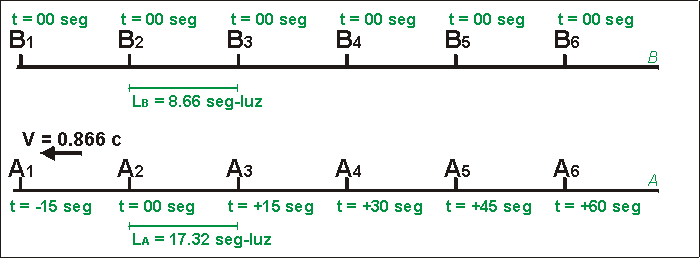 |
| Fig. 2 - Contrapartida de la Fig.1 tal como suele mostrarse en los libros de Relatividad Especial. Como veremos esta Figura es errónea. |
La Fig. 2 es absolutamente errónea y tiende a confundir a los estudiantes de la Relatividad.
El esquema correcto, para describir las observaciones del sistema B es el que se muestra en la Fig. 3.
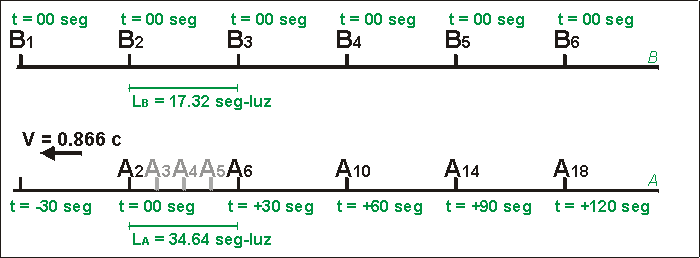 |
| Fig. 3 - Las cosas tal como son observadas desde el sistema B a t=00. |
En la Fig. 1 se observa que, de acuerdo con los observadores del eje A, a t=00, B3 se enfrenta con A3.
En la Fig. 3 se observa que, de acuerdo con los observadores del eje B, a t=00, B3 se enfrenta con A6.
Para entender esta diferencia de apreciaciones basta con seguir el desarrollo de los acontecimientos para los observadores de ambos ejes. Para ello asumiremos que el sistema A está realmente en reposo y que el eje B está realmente en movimiento.
La Fig.1 muestra las observaciones hechas desde el sistema A que tiene sus relojes perfectamente sincronizados mediante la constancia de c.
Pero el sistema B, también cree tener sus relojes perfectamente sincronizados en base a la constancia de c.
Como es de esperar, hasta que el reloj de B3 no marque t=00 no considera que el evento es simultáneo con la lectura del reloj de B2 cuando éste marcaba t=00.
Por lo tanto hay que seguir la secuencia de eventos mediante las Figs 4 a 6 hasta que el reloj de B3 marca t=00. Y, en ese instante (conforme a la simultaneidad del eje B) el observador enfrentado a B3 es A6.
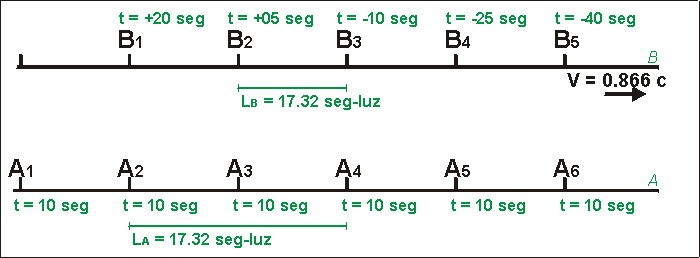 |
| Fig. 4 - La experiencia continúa. Los relojes marchan a velocidades diferentes. B3 se aleja de la posición de A2. |
En la Fig. 4 se observa que para el eje A transcurren 10 seg, mientras que (conforme al coeficiente de Lorentz de 0.5), para el eje B transcurren solamente 5 seg.
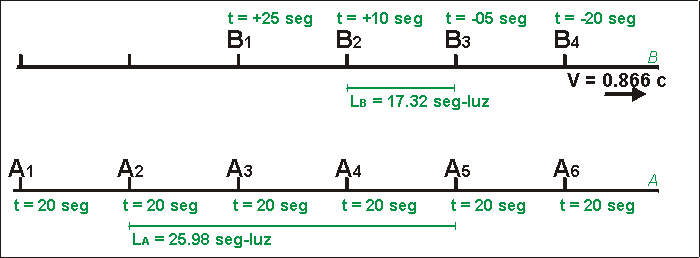 |
| Fig. 5 - La experiencia continúa. B3 ya está a 25.98 seg-luz de la posición de A2 pero su reloj aún no marca t=00 |
En la Fig. 5 B3 sigue alejándose de la posición de A2.
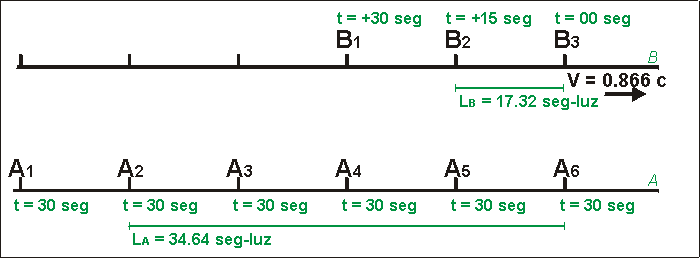 |
| Fig. 6 - Finalmente el reloj de B3 marca t=00. En ese momento se enfrenta con el reloj de A6 que marca t=30. La distancia (medida en A) que separa a A2 de A6 es el doble de la que separa a B2 de B3 (medida en B). |
Cuando B3 alcanza la posición de A6, su reloj marca t=00.
En resumen, para el eje B los hechos son los siguientes:
B2 y B3 están separados por 17.32 seg-luz (esta distancia la determinaron en base a la constancia de c).
Cuando el reloj de B2 marca t=00 se enfrenta con el reloj de A2 que también marca t=00.
Cuando el reloj de B3 marca t=00 se enfrenta con el reloj de A6 que marca t=30 seg.
Los observadores del eje A declaran que la distancia A2 - A6 es el doble que la que registran los observadores del eje B para la distancia B2 - B3.
Y, por lo tanto, la Fig. 3 y NO la Fig.2 es la contra-cara de la Fig.1
De este modo los 17.32 seg-luz que separan a los observadores B2 y B3, conforme a las mediciones del sistema B (basadas en la constancia de c), se corresponden con dos valores alternativos del sistema A:
Si esa distancia la miden observadores solidarios al sistema A, declaran que corresponde a 8.66 seg-luz, tal como muestra la Fig. 1
Si son los observadores de B los que usan esa separación entre B2 y B3 para determinar qué distancia cubre en el sistema A, obtienen una distancia que en A declaran que es de 34.64 seg-luz, tal como se explica en base a las Figs 1 y 4 a 6.
Siguiendo mi propio estilo, este desarrollo está hecho en forma gráfica y para valores numéricos específicos. Sin embargo es sólo una consecuencia de emplear las transformadas de Lorentz para sistemas en movimiento relativo. El empleo de un sistema realmente estacionario con relojes realmente sincronizados y un eje móvil con relojes des-sincronizados en base a las transformadas de Lorentz, permite visualizar la ausencia de sincronismo absoluto entre ambos sistemas. Y además demuestra, una vez más, que las ecuaciones relativistas son igualmente válidas para sistemas inerciales realmente equivalentes (Como postula la RE) o para sistemas inerciales sólo aparentemente equivalentes (como requiere el sentido común). :-)
En resumen,
Ambos sistema creen que las longitudes son la mitad de lo que declaran los observadores del otro sistema.
Las transformadas de Lorentz adoptan la misma forma para ambos sistemas, pero los valores absolutos NO SON LOS MISMOS !!.