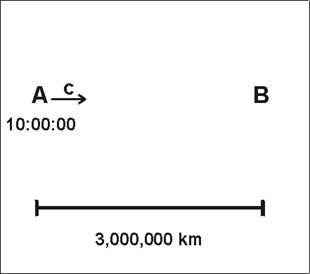
Fig. III-1: La señal electromagnética parte de A hacia B, cuando el reloj de A marca las 10:00:00
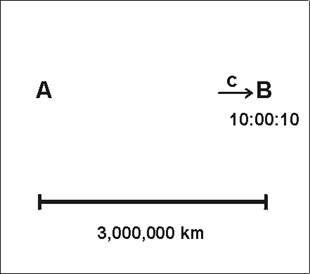
Fig. III-2: La señal electromagnética llega a B cuando el reloj de B marca las 10:00:10
“Es muy tarde para cambiar los planes – dijo Harry a
Hermione -.
No tenemos tiempo de enviar a Charlie otra lechuza... ”
J. K. Rowling – “Harry Potter y la Piedra Filosofal”
En el capítulo II se mostró la imposibilidad de lograr una simultaneidad absoluta con ondas sonoras o electromagnéticas. Dicho desarrollo puede ser llamativo pero los conceptos asociados, una vez explicados, no contradicen nuestra lógica convencional. Luego del análisis de detalle, resulta aceptable que sólo si la información se transmitiera a velocidad infinita se podría lograr una simultaneidad absoluta.
De este modo, aunque no existen velocidades infinitas, podemos imaginar lo que ocurriría si existieran. Y el resultado nos devuelve la “tranquilidad” mental. En otras palabras, no existe una simultaneidad absoluta, pero podemos imaginarla y atribuir la falta de simultaneidad práctica sólo a fenómenos de transmisión con velocidades limitadas.
Sin embargo, una vez que se acepta la falta de simultaneidad como hecho absoluto, se comienza a transitar por terrenos resbaladizos. De repente, otros conceptos que parecían naturales comienzan a generar desconfianza.
Uno de mis primeros recuerdos, asociados a las escalas astronómicas, se remonta al momento en que mi padre me comentó que la luz tarda unos 8 minutos en recorrer la distancia que separa a nuestro planeta del Sol. De esta forma, decía mi padre, si el Sol explotara en este momento, nosotros nos enteraríamos 8 minutos más tarde.
El concepto era llamativo, pero se podía entender. La información llegaba tarde, pero existía algo que nos permitía decir “en este momento” relacionando dos hechos separados por una enorme distancia.
Lo mismo ocurre con las noticias deportivas que se leen en los diarios al día siguiente de haber ocurrido. Nadie supone que la victoria de un equipo deportivo ocurre en el momento de leer la noticia en un diario. El hecho nos emociona en el momento que lo leemos, pero sabemos que aconteció en el pasado, en un momento “perfectamente” determinado. Hasta podemos decir qué es lo que estábamos haciendo en el momento que se desarrollaba el encuentro, quizás a miles de kilómetros de nuestra residencia.
Son los relojes los que nos permiten conocer la simultaneidad de eventos lejanos, aunque la noticia nos llegue con retraso.
Pero, esta simple afirmación da por sentado que los relojes marchan correctamente y están, por supuesto, correctamente sincronizados.
El siguiente es un ejemplo un poco más complejo, pero todavía cercano a nuestra experiencia cotidiana:
Si vemos que una piedra golpea con otra, a unos 340 m de distancia de nuestra posición, y el sonido nos alcanza con una demora de un segundo, podemos aceptar que todo se comporta de acuerdo con las leyes que conocemos puesto que la velocidad del sonido es de unos 340 m/s
Si por la existencia de un viento "en contra", el sonido se demora en llegar, no por eso diremos que se perdió la simultaneidad del golpe y de la generación de la señal sonora. Tampoco debemos concluir que el choque se produjo a más de 340 m porque la demora supera 1 s.
Sólo hay que aceptar que el sonido se demora como consecuencia de la velocidad del viento. Esto no es más que física clásica, y la Relatividad Especial no se opone a la física clásica.
Lo que analizaremos desde sus orígenes, en esta obra, es ¿Cómo sabemos que el suceso ocurrió a 340 m de distancia?
Analizando estos supuestos básicos, Einstein, llegó a la asombrosa conclusión (¿Intuición genial?) de que para medir distancias estamos “obligados” a emplear fenómenos electromagnéticos (luz, en su versión más popular). Y ya sabemos que la velocidad de la luz, aunque muy grande, no evita la falta de simultaneidad absoluta.
Es conveniente mencionar nuevamente que, con excepción de la fuerza de gravedad, todas las demás interacciones que observamos en el mundo físico son electromagnéticas. La otra excepción la constituyen las fuerzas nucleares pero no las observamos regularmente.
Cuando una pelota rebota en el suelo, lo hace como consecuencia de la interacción de las capas de electrones de los átomos de la pelota y de los constituyentes del suelo. El color, el calor, las reacciones químicas, los rebotes, el sonido, la música, el envejecimiento, etc., son resultado de interacciones electromagnéticas.
En este punto, teniendo en cuenta su importancia conceptual, parece adecuado transcribir un párrafo de Einstein, en la introducción de su trabajo inicial sobre la Relatividad Especial:
"…La teoría a desarrollar se basa -como toda la electrodinámica- en la cinemática del cuerpo rígido dado que las afirmaciones de tales teorías están vinculadas a las relaciones entre cuerpos rígidos (sistemas de coordenadas), relojes y procesos electromagnéticos. La raíz de las dificultades que encuentra, en el presente, la electrodinámica de los cuerpos en movimiento yace en una insuficiente consideración de estas circunstancias…".
Y…, a riesgo de exagerar en la importancia de los conceptos fundamentales, quiero rescatar del párrafo anterior la enumeración "...cuerpos rígidos (sistemas de coordenadas), relojes y procesos electromagnéticos..." cómo base de todo el andamiaje físico que estamos discutiendo. Esta síntesis asombrosa, habla por si sola de la capacidad de Einstein para llegar a los fundamentos teóricos.
Supongamos que hemos determinado que cierto observador, identificado como B, se encuentra a 3,000,000 km de otro al que llamamos A. Para ello habremos usado una regla de 1 m o algún proceso de triangulación que se basa en la regla de 1 m.
Dado que se trata de un ejemplo imaginario, podemos suponer que B se alejó caminando de la posición de A y fue midiendo, con la regla de 1 m, la distancia recorrida hasta alcanzar su nueva posición, a 3,000,000 de km de A.
También podemos suponer que B y A poseen relojes de excelente construcción, idénticos en todo sentido y perfectamente sincronizados en el momento de separarse.
Una vez alcanzada su nueva posición relativa, A y B realizan una medición de comprobación de sus relojes mediante la siguiente secuencia de eventos y mediciones.
|
|
|
|
Fig. III-1: La señal electromagnética parte de A hacia B, cuando el reloj de A marca las 10:00:00 |
Fig. III-2: La señal electromagnética llega a B cuando el reloj de B marca las 10:00:10 |
A manda una señal de radio hacia B, indicando que su reloj marca las 10:00:00 (Fig. III-1). La señal de radio está constituida por ondas electromagnéticas que se trasladan a igual velocidad que la luz. A esta lectura del reloj de A la llamamos Ta.
La señal tarda 10 segundos en recorrer los 3,000,000 km que separan a B de A.
B recibe la señal cuando su propio reloj marca las 10:00:10 (tiempo Tb) y devuelve la señal, en forma inmediata, en dirección a la posición de A (Fig. III-2 y Fig. III-3).
La señal tarda otros 10 segundos en recorrer los 3,000,000 km que separan a los dos observadores.
A recibe la señal de respuesta cuando su propio reloj marca las 10:00:20. A esta lectura del reloj de A la llamamos T’a (Fig. III-4).
|
|
|
|
Fig. III-3: B devuelve la señal en forma inmediata. |
Fig. III-4: La señal electromagnética retorna a A cuando el reloj de A marca las 10:00:20. |
De esta forma A y B comprueban que:
El tiempo total invertido por la señal en su viaje de ida y vuelta (T’a –Ta = 20 s) es el correcto para un recorrido de 6,000,000 km a 300,000 km/s.
Sus relojes permanecen sincronizados, aún después del traslado
La luz invierte el mismo tiempo (10 s) en hacer el recorrido de A hacia B (ida) y de B hacia A (vuelta).
Nota: Si la lectura Tb hubiera sido diferente a la indicada, los observadores hubieran supuesto que el reloj de B se desacomodó durante el traslado y hubieran reajustado la hora de dicho reloj para recuperar el sincronismo de sus lecturas.
Puede afirmarse, sobre la base de toda la experiencia acumulada en el traslado terrestre de relojes, la colocación en órbita de relojes de elevada precisión para el sistema de posicionamiento global (GPS), etc., que, en caso de que pudiera realizarse una experiencia como la detallada en este experimento imaginario, los resultados serían los indicados. De hecho, variantes de este experimento imaginario se llevan a cabo, rutinariamente, con el instrumental que se envía en las naves espaciales y se comanda desde La Tierra teniendo en cuenta las demoras en la recepción de las señales electromagnéticas.
Otra forma de expresar el resultado de este experimento imaginario es diciendo que todo se comporta como si los observadores A y B estuvieran en reposo con respecto al medio soporte que permite el traslado de las ondas luminosas. La luz se traslada a velocidad c tanto en el viaje de ida como en el viaje de vuelta, indicando que, si existiera un medio soporte, todo sucede como si los observadores estuvieran en reposo con respecto al mismo.
Usando una terminología simple, podemos decir que el resultado de la experiencia se explica si “v = 0”, siendo “v“ la velocidad de los observadores con respecto al medio soporte.
Nota: El siguiente desarrollo está muy simplificado. Como se verá en otros capítulos, y como seguramente notarán quienes conocen en detalle los desarrollos de la Relatividad Especial, sólo voy a considerar parcialmente los fenómenos relativistas. De todos modos este planteo limitado sirve para analizar y discutir el concepto de sincronismo de relojes lejanos.
Si, después de hacer la experiencia ya analizada, tanto A como B emprenden un viaje a alta velocidad, podemos analizar, hipotéticamente, lo que ocurriría con el sincronismo de sus relojes.
La experiencia se programa, de modo que ambos observadores adquieran una velocidad v = 200,000 km/s en la dirección que define la recta que los une y en el sentido AB. La secuencia de eventos puede resumirse de la siguiente forma:
A y B aceleran, con naves adecuadas e idénticos procedimientos, a partir de una hora prefijada, hasta adquirir la velocidad de 200,000 km/s respecto de los observadores que permanecen en el sistema en que A y B habían hecho sus mediciones iniciales. A estos otros observadores (no sometidos a aceleraciones en toda la experiencia) los llamaremos observadores estacionarios.
Una vez alcanzada la velocidad preestablecida, ambos viajeros detienen la aceleración y continúan su desplazamiento en condiciones inerciales.
Los observadores estacionarios comprueban que todas las operaciones salieron de acuerdo con lo planeado. También verifican que ambos viajeros ahora se desplazan a 200,000 km/s respecto de ellos y que la distancia que los separa sigue siendo 3,000,000 km, como cuando estaban en reposo.
Llegados a este punto A y B repiten la operación de sincronizado de sus relojes, siguiendo los mismos procedimientos que en el primer ejemplo.
|
|
|
Fig. III-5: Tal como lo aprecian los observadores estacionarios, cuando A y B están en movimiento, la señal recorre la separación entre ambos a diferentes velocidades. |
Pero…, las condiciones han cambiado. La Fig. III-5 muestra la experiencia tal como la ven los observadores estacionarios. El rayo de luz que parte de A hacia B se aleja de A a una velocidad de sólo 100,000 km/s, dado que A avanza en el mismo sentido que el rayo luminoso a una fracción apreciable de su velocidad.
c = 300,000 km/s
v = 200,000 km/s
c – v = 100,000 km/s
Recordemos que la velocidad de la luz no depende de la velocidad de la fuente, de modo que, para los observadores estacionarios, la velocidad de la señal electromagnética emitida por A es de 300,000 km/s y avanza en el mismo sentido en que lo hace A a 200,000 km/s
Esto hace que la señal tarde 30 s (siempre de acuerdo con los observadores estacionarios) en alcanzar la posición de B.
3,000,000 km
-------------------------- = 30 s
100,000 km/s
Para el retorno de la señal, la velocidad de desplazamiento de A y B se suma a la velocidad de la señal (Fig. III-5).
c = 300,000 km/s
v = 200,000 km/s
c + v = 500,000 km/s
De esta forma, el tiempo de retorno de la señal hasta la posición de A es de sólo 6 s.
Siempre estamos hablando de las mediciones efectuadas por los observadores estacionarios.
3,000,000 km
-------------------------- = 6 s
500,000 km/s
Como consecuencia de este análisis simple, resulta que la señal tarda un tiempo diferente en recorrer el camino de ida de A hacia B, que en hacer el camino de retorno. Además, el tiempo total de viaje de la señal (30 s + 6 s = 36 s) es diferente del que se empleaba antes de la aceleración de los viajeros (20 s).
Nota: Todas las mediciones de tiempos y distancias indicadas están hechas por los observadores estacionarios. Los resultados indicados son rigurosamente los que se obtendrían en una medición real. Sin embargo, como veremos a lo largo de esta obra, estos resultados no tienen por que ser los mismos que aprecian los observadores sometidos al proceso de aceleración.
Pregunta: El hecho de sumar velocidades a la velocidad de la luz, ¿No contradice los postulados relativistas?
Respuesta: No, las expresiones (c + v) y (c - v), empleadas incluso por Einstein en sus desarrollos de 1905, son perfectamente válidas para mostrar la información que recogen los observadores estacionarios. Estas ecuaciones simples son, por ejemplo, la base de uso de los giróscopos ópticos. Para lo que no sirven estas adiciones de velocidad es para describir lo que registran los observadores en movimiento con respecto al mismo rayo de luz.
Podemos resumir ambas experiencias en los siguientes términos.
Los tiempos empleados por las señales electromagnéticas para recorrer una distancia en reposo, medida por dichos observadores, son consistentes con una velocidad de la luz constante (c = 300,000 km/s) tanto en viajes de ida como de vuelta.
Los tiempos empleados por las señales electromagnéticas para recorrer la misma distancia, pero en movimiento respecto de los mismos observadores, son diferentes para la ida y para la vuelta. Además el tiempo total empleado en hacer el recorrido de ida y vuelta es mayor que el registrado durante la medición en reposo.
Por extraño que pueda parecer a quienes lo analizan por primera vez, la constancia de c se mantiene aún para los observadores A y B, luego de haber acelerado.
Expresado de otra forma, si A y B fueran dos físicos experimentales y hubieran llevado consigo todo el instrumental necesario para medir el valor de c, descubrirían, luego del proceso de aceleración, que la velocidad de la luz, respecto a ellos, sigue siendo de 300,000 km/s.
Esta observación no coincide con lo que aprecian los observadores estacionarios, no sometidos a aceleración durante las experiencias. Como ya se indicó, para estos observadores, la luz se traslada a 500,000 km/s ó 100,000 km/s respecto de A y de B.
Más aún, si A y B hubieran sido acelerados antes de separarse y B hubiera emprendido su caminata de 3,000,000 km una vez alcanzada la velocidad de 200,000 km/s respecto al sistema al que pertenecían originalmente, hubieran registrado exactamente los mismos resultados experimentales que se indican para la experiencia en reposo. El sincronismo de sus relojes se hubiera mantenido y la luz mostraría la misma velocidad (300,000 km/s) para el viaje de ida y el de vuelta.
Nota: Está claro que esta experiencia no se ha llevado a cabo en los términos expresados. Sin embargo, toda la experiencia acumulada indica que los resultados consignados son los que se esperan en función de las propiedades físicas del Universo conocido.
En realidad este apartado está rotulado como “dato experimental” para no someterlo a discusión. Los “datos” consignados no resultan de una mera hipótesis de trabajo. Son la consecuencia de rigurosas mediciones de la velocidad de la luz en una increíble variedad de circunstancias.
Adicionalmente, tanto la teoría como la experiencia muestran que, cuando se trasladan relojes a baja velocidad, éstos no pierden su sincronismo. En el Capítulo IX este tema se trata con sumo detalle.
Veamos las aparentes inconsistencias que generan los resultados discutidos hasta este punto.
Debe recordarse que el tiempo total de viaje de la señal se registra con las lecturas inicial y final en el reloj de A. El reloj de B no interviene en esta medición.
Si el reloj de A, luego de acelerar, siguiera marchando al mismo ritmo que cuando estaban en el sistema denominado estacionario, también registraría 36 s, para el viaje de ida y vuelta del rayo luminoso.
En consecuencia, A y B estarían de acuerdo en que la distancia que los separa es de:
300,000 km/s x 36 s / 2 = 5,400,000 km
Este resultado sería difícil de justificar basándose en la forma en que se condujo el experimento. A y B esperan estar separados por 3,000,000 km luego del período de aceleración.
El apartado previo sugiere que la marcha de los relojes puede haberse alterado durante el proceso de aceleración. Aunque este punto se analiza con mucho más detalle en los próximos capítulos, por ahora basta decir que, en caso de existir una alteración, ésta debe ser la misma para los relojes de ambos observadores, dado que fueron sometidos a idénticos procesos.
De este modo si los ritmos de ambos relojes fueran más lentos (esta es la forma más sencilla en que A y B creerían que transcurren menos de 36 s en el viaje de ida y vuelta de la señal), aún mantendrían la misma marcha de uno respecto del otro.
Pero..., esto también genera una inconsistencia. Si los relojes de A y B mantuvieran las mismas lecturas, medidas desde el sistema estacionario, A y B podrían comprobar que el viaje de ida de la señal es de mayor duración que el viaje de vuelta.
Nota: Si los ritmos fueran diferentes a los de los relojes estacionarios, A y B no registrarían 3 s y 6 s para estos trayectos pero obtendrían números proporcionales a dichos valores, manteniendo una diferencia significativa entre el tiempo de ida y de regreso de la señal.
La única forma (siempre desde la óptica de los observadores estacionarios) en que A y B pueden sostener la constancia del valor de c tanto en el viaje de ida como en el de vuelta es “atrasando” la lectura del reloj de B. De esta forma, el reloj de B no registraría todo el tiempo transcurrido en el viaje de ida de la señal, sino sólo una fracción del mismo.
El “atraso” debe ser tal que parezca que la señal llega a B justo a la mitad del intervalo total registrado por el reloj de A para el viaje de ida y vuelta. Otra vez es conveniente mencionar que este tema se trata con mucho más detalle en los próximos capítulos.
El análisis presentado nos lleva a la conclusión de que la constancia de c resulta inconsistente con ritmos y sincronismos absolutos para relojes en diferentes estados de movimiento.
Aún no hemos analizado la Relatividad en detalle, pero ya hemos tropezado con algunas de sus consecuencias principales.
Y..., aunque ya podemos apreciarlo, en el capítulo IV veremos que los problemas con los tiempos desembocan, inevitablemente, en problemas con las longitudes.
El lector imbuido de los conceptos relativistas podrá apreciar que lo que estoy haciendo es justificar, con argumentos más o menos complejos, los conocidos resultados de la Teoría de Einstein.
Por otra parte, el lector desprevenido puede suponer que he hecho algunos malabarismos para justificar lo injustificable.
Sin embargo es fácil identificar cuál es el supuesto que genera la situación planteada: Para poder sostener la constancia de c, para todos los observadores inerciales, es necesario que las lecturas de tiempos y longitudes varíen entre uno y otro observador.
Por supuesto Einstein comprendió perfectamente este punto y lo resaltó en su trabajo de 1905. Sin embargo la costumbre ha hecho que la constancia de c resulte un hecho natural y perfectamente aceptable.
Al presentar los dos postulados que conducen a la Relatividad Especial, Einstein empleó la siguiente expresión:
".... como ya fue mostrado hasta el primer orden de cantidades pequeñas, que las mismas leyes de la electrodinámica y la óptica son válidas en todos los sistemas de referencia en los cuales las leyes de la mecánica funcionan bien. Nosotros elevaremos esta conjetura (a cuyo significado haremos referencia como "Principio de Relatividad") al "status" de Postulado y también introduciremos un segundo postulado que es sólo aparentemente irreconciliable con el primero.... "
Y de esta introducción quiero rescatar el párrafo "... un segundo postulado que es sólo aparentemente irreconciliable con el primero...", pues muchos estudiosos parecen no notar la contradicción latente entre ambos postulados.
Esta contradicción es muy difícil de apreciar en la actualidad pues todos, desde muy pequeños, "sabemos" que la velocidad de la luz es constante, del mismo modo que "sabemos" que el Sol es sólo una estrella más, también "sabemos" que la materia está formada por átomos y "sabemos" (entre otras muchas cosas) que la Tierra da vueltas alrededor del Sol y no el Sol alrededor de la Tierra.
Nota: Utilizo comillas en la palabra "sabemos" pues hace referencia a un conocimiento que adquirimos sin pasar por un proceso crítico de aprendizaje. Estos conocimientos "primarios" parecen absolutamente obvios e indiscutibles en la edad adulta.
Para emplear un ejemplo que permita apreciar la razón por la cual Einstein creyó necesario hacer el comentario mencionado, voy a utilizar un símil geométrico de ambos postulados.
Supongamos que queremos medir la distancia vertical entre todos los objetos de la superficie terrestre y la distancia que los separa del centro de la Tierra.
Sobre la superficie de la Tierra existen innumerables observadores estacionarios y también móviles, de modo que, para evitar problemas de cambios en el nivel de referencia, elegimos sólo observadores estacionarios (inmóviles con respecto a la superficie terrestre). A continuación, a cada observador le entregamos reglas idénticas y todos los aparatos de medición que le resulten necesarios para la tarea.
Como resultado de estas mediciones algún observador dirá que un determinado objeto está 500 m más arriba de su propia posición y otro dirá que ese mismo objeto está 100 m por debajo de la suya propia.
Ambas descripciones resultan válidas, siempre y cuando cada observador emplee siempre el mismo nivel de referencia. Esta es la razón de evitar el empleo de observadores que se estén desplazando por la superficie terrestre.
De modo que estamos en condiciones de proponer nuestro primer postulado para las mediciones de nivel de los objetos de la superficie terrestre.
Las leyes que describen los cambios de nivel entre objetos de la superficie terrestre no resultan afectadas si estos cambios de nivel se refieren a uno u otro de dos sistemas de coordenadas estacionarios.
No es difícil aceptar la validez de este postulado. Cada observador tiene su propio nivel de referencia, pero todas las observaciones respecto a niveles relativos, entre objetos de la superficie terrestre, serán igualmente adecuadas.
Ningún observador afirmará que el techo de las casas está por debajo del nivel del piso.
Pero qué pasaría si introducimos un segundo postulado estableciendo:
La distancia que separa a cualquier observador estacionario del centro de la Tierra es de 6,400 km.
Este segundo postulado parece irreconciliable con el primero, pues si bien todos los observadores pueden medir niveles diferentes entre ellos, resulta que TODOS están al mismo nivel con respecto al centro de la Tierra. De esta forma, un observador en la superficie del mar y otro ubicado en la cima del monte Everest estarían a la misma distancia del centro de la Tierra.
Por supuesto que el segundo postulado del ejemplo empleado es insostenible. Pero lo mismo pasaba, en el momento de su introducción, con el postulado de la constancia de c para todos los observadores inerciales:
El primer postulado de la Relatividad Especial permite medir todo tipo de velocidades relativas entre observadores inerciales
Pero…, el segundo postulado exige que la velocidad de la luz sea la misma para todos ellos.
Conforme a los dos postulados de Einstein, un rayo de luz, que se mueve a 300,000 km/s con respecto a un observador inercial, también se mueve a 300,000 km/s con respecto a otro que se desplaza, en cualquier dirección, a 200,000 km/s con respecto al primero.
Sin embargo, es necesario recordar que el postulado de la constancia de la velocidad de la luz no fue introducido arbitrariamente. Por el contrario, este postulado se basó en una muy sólida documentación experimental que atestiguaba la imposibilidad de detectar cambios en el valor de c empleando observadores inerciales con diferentes velocidades relativas.
La reconciliación matemática de ambos postulados fue desarrollada por Einstein en 1905 y dio lugar a lo que se conoce como Relatividad Especial o Restringida.
La reconciliación conceptual es la que todavía está esperando su lugar en la física.
Justamente, la reconciliación conceptual de ambos postulados relativistas es el objetivo primario de esta obra.